Pour continuer notre périple en cryptographie, je vous propose d’aborder aujourd’hui le Cryptosystème de ElGamal.

Présenté en août 1984 par Taher Elgamal, d’où l’algorithme tiens son nom, il propose un protocole de chiffrement asymétrique construit à partir de l’Échange de clés Diffie-Hellman (Publié 8 ans plus tôt).

A Public Key Cryptosystem and a Signature Scheme Based on Discrete Logarithms, ElGamal T. Lecture Notes in Computer Science, vol 196. (PDF).

Rappel de Diffie Hellman

Le plus simple pour comprendre ElGamal, c’est encore de repartir de l’échange de clé Diffie-Hellman. Pour rappel, voici les étapes du protocole :

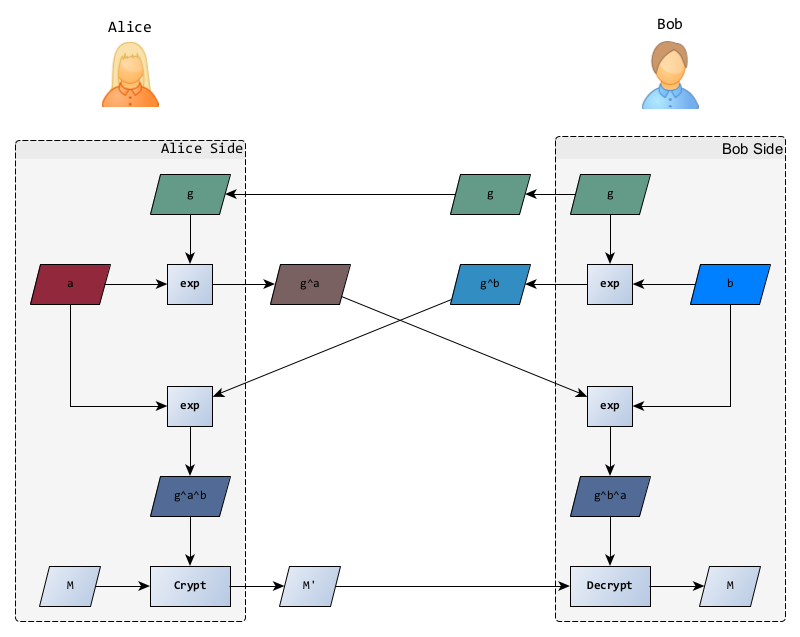
1. Alice et Bob se mettent d’accord publiquement sur un groupe $(G, \times)$ et un générateur $g$ ;
2. Ils choisissent chacun un nombre aléatoire (leur clé secrète), $a$ pour Alice et $b$ pour Bob ;
3. Ils calculent leur partie publique et se l’envoie l’un l’autre ; Alice envoie donc $g^a$ à Bob et reçoit $g^b$ en retour ;
4. Ils calculent enfin le secret partagé ; Alice calcule $g^{b^a}$ et Bob calcule $g^{a^b}$ qui, magie des mathématiques, ont la même valeur.
5. Ils peuvent maintenant utiliser ce secret partagé pour chiffrer et déchiffrer leurs communications suivantes 🎉.

ElGamal

Pour Elgamal, le protocole est exactement le même mais comme seule Alice a besoin d’écrire à Bob, ils peuvent se répartir le protocole et prendre des initiatives.

Préliminaires

Pour permettre à tout un chacun de lui envoyer des mots gentils, Bob se charge de la première moitié du protocole :

• choix du groupe $(G, \times)$,
• choix du générateur $g$,
• choix d’un nombres aléatoire secret $b$,
• calcul de la partie publique $g^b$.

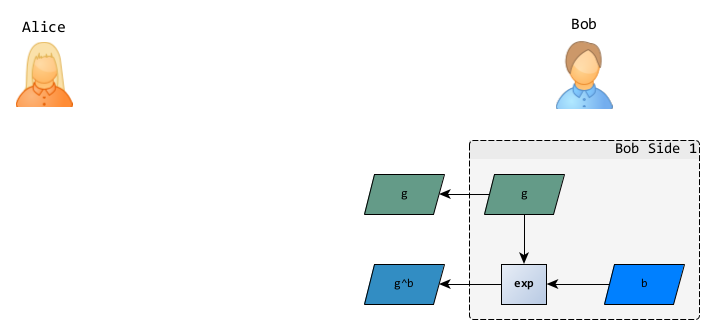
Les informations publiques (groupe, générateur et $g^b$) constituent la clé publique et peuvent être envoyées à l’avance à Alice ou carrément publiées sur un annuaire pour que tout le monde en profite.

Génération du message secret

Pour envoyer un message à Bob, Alice récupère ces informations publiques et se charge de la deuxième partie du protocole :

• choix de son nombre aléatoire secret $a$,
• calcul de sa partie publique $g^a$,
• calcul du secret partagé $g^{b^a}$,
• chiffrement du message $m' = m . g^{b^a}$

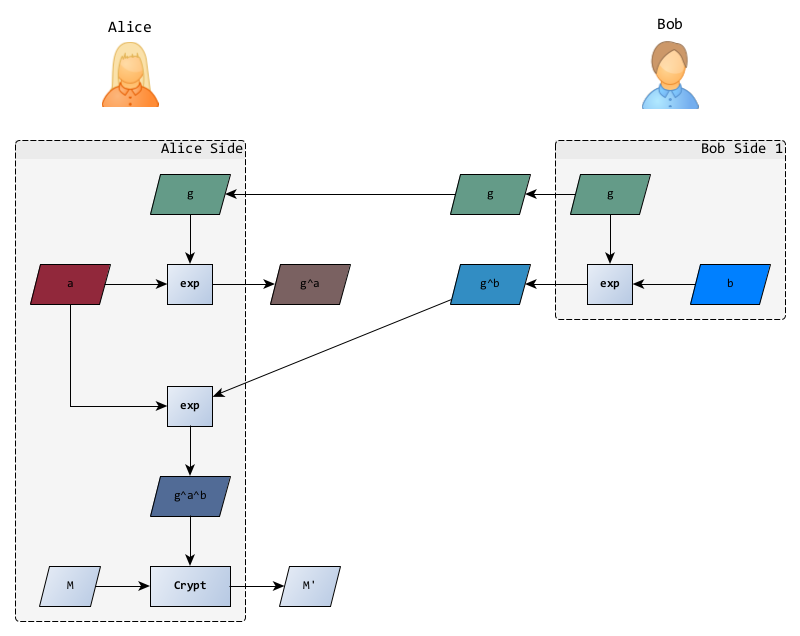
Dans l’article original d’Elgamal, le chiffrement s’effectue dans un groupe fini additif ou multiplicatif, l’important étant qu’il soit facilement inversible. C’est habituellement une multiplication qui est choisie.

Elle n’a plus qu’à envoyer sa partie publique et le message chiffré à Bob.

Réception du message

Avec toutes ces informations, Bob peut calculer la clés secrète et déchiffrer le message.

• calcul du secret partagé $g^{a^b}$
• déchiffrement du message $m = m' / g^{a^b}$

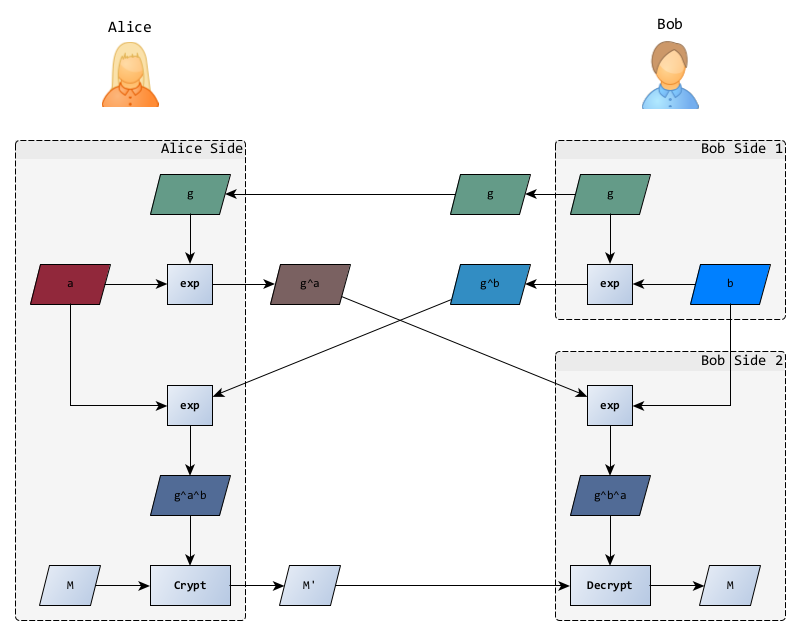
Si vous ne voyez pas la parenté avec Diffie Hellman, revenez au premier schéma 😉.

En vrai…

Tout ça, c’est en théorie car en pratique, il y a quelques petites adaptations.

Ajout d’une PKI

Tant que Eve ne peut qu’écouter le réseau, tout va bien mais si elle est capable de modifier les communications, elle peut très bien remplacer les clés d’Alice et de Bob par la sienne dans les échanges.

Lorsqu’Alice croit envoyer un message à Bob, elle l’envoie en fait à Eve qui peut le déchiffrer. Après l’avoir lu, elle le chiffre avec sa propre clé à destination de Bob. Notez qu’elle peut aussi modifier le contenu avant de chiffrer et d’envoyer à Bob.

Le message que Bob reçoit étant accompagné de la clé publique permettant de le déchiffrer, il ne peut pas être sûr de qui en est l’auteur (uniquement qu’il en est bien le destinataire).

Pour résoudre ce problème (déjà présent pour Diffie hellman), on utilise alors des signatures et un tiers de confiance qui se charge d’authentifier les clés publiques des acteurs. Souvent en signant des certificats mais pas que.

Système hybride

L’opération de chiffrement et déchiffrement est possible sur des messages arbitrairement longs mais cette opération reste souvent plus lente que les algorithmes de chiffrement symétriques ayant une sécurité équivalente.

On aurait pu remplacer la multiplication par un algorithme symétrique, le secret partagé étant alors la clé de cet algorithme, mais l’usage en a choisi autrement (et a bien fait).

En effet, on préfère utiliser l’algorithme d’Elgamal, inchangé, conjointement à un algorithme symétrique. On parle alors d’algorithme hybdide. On choisi alors une clé pour chiffrer le message et c’est cette clé qui sera chiffrée avec Elgamal.

L’avantage de cette méthode, est de découpler l’algorithme asymétrique qui établi la communication (Elgamal, RSA, …), et l’algorithme symétrique qui sécurise le contenu (AES, 3DES, …). Il est alors possible de choisir la combinaison la plus adaptée ou de faire évoluer une partie en fonction des dernières avancées.

C’est ce qui est fait au travers des cypher suites de TLS et qui a encore été renforcé dans la version 1.3 du protocole (RFC8446).

Nonce Re-use

Lorsqu’Alice veut envoyer un message à Bob, elle doit générer un nombre aléatoire secret $a$ spécifique pour le message à envoyer.

Elle pourrait bien sûr réutiliser la clé précédente mais ce faisant, elle mettrait en péril la sécurité de tous ses échanges.

En effet, admettons qu’Alice envoie deux messages $m_1$ et $m_2$ à Bob en utilisant le même nombre aléatoire $a$. Bob n’ayant pas changé sa clé publique, le secret partagé ($K = g^{b^a}$) sera le même pour le chiffrement des deux messages :

$$\begin{align} m_1' & = m_1 . K \\ m_2' & = m_2 . K \end{align}$$

Admettons maintenant qu’une attaquante (Eve) ai mis la main sur un message en clair… (prenons $m_1$). Le problème, c’est qu’ainsi, elle pourra s’en servir pour déchiffrer tous les autres messages entre Alice et Bob. $$\begin{align} m_1' / m_2' & = (m_1 . K) / (m_2 . K) \\ m_2 & = m_1 . m_2' / m_1' \end{align}$$

Ce qui peut arriver plus souvent qu’on le croit… L’attaque Krack sur le WPA2 suit cette même logique (même si le chiffrement utilisé est différent). Forcer les clients WIFI à utiliser un nonce plusieurs fois puis, grâce à la connaissance (partielle) d’un message clair, déchiffrer les autres.

Notez que dans ce cas, Eve peut aussi retrouver le secret partagé $K$ : $$\begin{align} K & = m' / m \end{align}$$

Heureusement, même en possession des parties publiques et du secret partagé, obtenir les clés privées reste difficile puisqu’il s’agit de résoudre le problème du logarithme discret.

En fait, il s’agit de résoudre le problème de Diffie-Hellman qui en l’état actuel de nos connaissance est aussi difficile que celui du logarithme discret.

Attaque sur le chiffré

Tel que défini et utilisé, ce chiffrement possède la propriété de malléabilité : il est possible, dans un certaine mesure, de modifier le message clair en n’opérant que sur le chiffré.

Précisément, l’opération de chiffrement étant une multiplication, multiplier le chiffré par une constante a le même effet que si la multiplication avait eu lieu sur le clair :

$$\begin{align} n . m' & = n . m . K = (n . m)' \end{align}$$

Si Elgamal est utilisé pour chiffrer un message, et que Eve à la possibilité d’intercepter les communication, elle peut alors modifier le contenu même des messages et en fonction des contextes, en changer le sens à son avantage.

Pour éviter ce type d’attaque, on peut soit ajouter un système de signature au messages ou le gérer directement dans le protocole comme c’est le cas avec Cramer-Shoup.

Si El Gamal est utilisé pour chiffrer une clé symétrique, cette faiblesse n’est plus très pertinente puisque changer la clé symétrique rendra le message illisible, ce que Eve aurait tout aussi bien pu obtenir en remplaçant le message par des données aléatoires.

Enfin, il faut noter que cette propriété n’est pas spécifique à El Gamal mais touche aussi d’autres protocoles comme RSA ou dans une moindre mesure le mode CBC.

Et après ?

Au moment de sa publication, RSA était couvert par un brevet (brevet US4405829A, valable uniquement aux US car déposé après une publication) et la communauté a été bien contente d’accueillir un nouvel algorithme libre de droits. GnuPG, le clone libre de PGP implémente donc ce cryptosystème pour les échanges de messages.

Par contre, El Gamal ne propose pas nativement de méthode de signature. Il n’est donc pas utilisable pour certaines applications comme SSL/TLS pour lesquels RSA garde l’avantages, surtout depuis l’expiration du brevet en septembre 2000.

D’un autre côté, comme on peut implémenter Elgamal sur n’importe quel groupe fini, une version sur courbes elliptique a pu voir le jours (i.e. implémentée dans GnuPG) et propose, à taille de clé équivalente, une sécurité largement supérieure.

Pour terminer, voici les recommandations de l’ANSSI (via son Référentiel Général de Sécurité) en matière de longueur de clés pour les chiffrements asymétriques :

• Pour la version classique, 2048 bits avant 2030 et 3072 bits au delà.
• Pour la version sur courbes elliptiques, 200 bits avant 2020 et 256 bits au delà.

En vrai, on utilise rarement ElGamal, mais sa filiation avec Diffie-Hellman le rend facilement compréhensible et lui permet une implémentation via courbes elliptiques, plutôt à la mode et bien pratique.